Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Ex 3.1

Students can Download Maths Chapter 3 Algebra Ex 3.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Ex 3.1

Question 1.
Fill in the blanks.

1. The exponential form 14⁹ should be read as ______
2. The expanded form of p³ q² is ______
3. When base is 12 and exponent is 17, its e×ponential form is _____
4. The value of (14 × 21)⁰ is _____

Answers:

1. 14 Power 9
2. p × p × p × q × q
3. 12¹⁷
4. 1

Question 2.
Say True or False.

1. 2³ × 3² = 65
2. 2⁹ × 3² = (2 × 3)^9×2
3. 3⁴ × 3⁷= 3¹¹
4. 2⁰ × 1000⁰
5. 2³ < 3²

Answers:

1. False
2. False
3. True
4. True
5. True

Question 3.
Find the value of the following.

1. 2⁶
2. 11²
3. 5⁴
4. 9³

Solution:

1. 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64
2. 11² = 11 × 11 = 121
3. 5⁴ = 5 × 5 × 5 × 5 = 625
4. 9³ = 9 × 9 × 9 = 729

Question 4.
Express the following in e×ponential form.

1. 6 × 6 × 6 × 6
2. t × t
3. 5 × 5 × 7 × 7 × 7
4. 2 × 2 × a × a

Solution:

1. 6 × 6 × 6 × 6 = 6^1+1+1+1 = 64 [Since a^m × aⁿ = a^m+n]
2. t × t = t¹⁺¹ = t²
3. 5 × 5 × 7 × 7 × 7 = 5¹⁺¹ × 7¹⁺¹⁺¹ = 5² × 7³
4. 2 × 2 × a × a = 2¹⁺¹ × a¹⁺¹ = 2² × a² = (2a)²

Question 5.
E×press each of the following numbers using e×ponential form,
(i) 512
(ii) 343
(iii) 729
(iv) 3125
Solution:
(i) 512

512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2⁹ [Using product rule]

(ii) 343

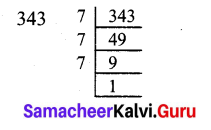
343 = 7 × 7 × 7 = 7¹⁺¹⁺¹
= 7³ [Using product rule]

(iii) 729

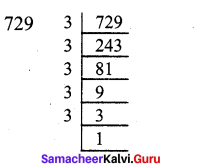
729 = 3 × 3 × 3 × 3 × 3 × 3
= 3⁶ [Using product rule]

(iv) 3125

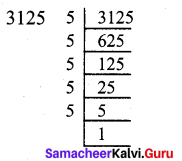
3125 = 5 × 5 × 5 × 5 × 5
= 5⁵ [Using product rule]

Question 6.
Identify the greater number in each of the following.
(i) 6³ or 3⁶
(ii) 5³ or 3⁵
(iii) 2⁸ or 8²
Solution:
(i) 6³ or 3⁶
6³ = 6 × 6 × 6 = 36 × 6 = 216
3⁶ = 3 × 3 × 3 × 3 × 3 × 3 = 729
729 > 216 gives 3⁶ > 6³
∴ 36 is greater.

(ii) 5³ or 3⁵
5³ = 5 × 5 × 5 = 125
3⁵ = 3 × 3 × 3 × 3 × 3 = 243
243 > 125 gives 3⁵ > 5³
∴ 3⁵ is greater.

(iii) 2⁸ or 8²
2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
8² = 8 × 8 = 64
256 > 64 gives 2⁸ > 8²
∴ 2⁸ is greater.

Question 7.
Simplify the following
(i) 7² × 3⁴
(ii) 3² × 2⁴
(iii) 5² × 10⁴
Solution:
(i) 7² × 3⁴ = (7 × 7) × (3 × 3 × 3 × 3)
= 49 × 81 = 3969

(ii) 3² × 2⁴ = (3 × 3) × (2 × 2 × 2 × 2)
= 9 × 16 = 144

(iii) 5² × 10⁴ = (5 × 5) × (10 × 10 × 10 × 10)
= 25 × 10000 = 2,50,000

Question 8.
Find the value of the following.
(i) (-4)²
(ii) (-3) × (-2)³
(iii) (-2)³ × (-10)³
Solution:
(i) (-4)² = (-1)² × (4)² [since a^m × b^m = (a × b)^m]
= 1 × 16 = 16 [since (-1)ⁿ = 1 if n is even]

(ii) (-3) × (-2)³ = (-1) × (-3) × (-1)³ × (-2)³
= (-1)⁴ × 24 [Grouping the terms of same base]
= 24

(iii) (-2)³ × (-10)³ = (-1)³ × (-2)³ × (-1)³ × (-10)³
= (-1)³⁺³ × 2³ × 10³ [Grouping the terms of same base]
= (-1)⁶ × (2 × 10)³
[∵ a^m × b^m = (a × b)^m]
= 1 × 20³ [since (-1)ⁿ = 1 if n is even]
= 8000

Question 9.
Simplify using laws of exponents.
(i) 3⁵ × 3⁸
(ii) a⁴ × a¹⁰
(iii) 7x × 7²
(iv) 2⁵ ÷ 2³
(v) 18⁸ ÷ 18⁴
(vi) (6⁴)³
(vii) (x^m)⁰
(viii) 9⁵ × 3⁵
(ix) 3^y × 12^y
(x) 25⁶ × 5⁶
Solution:

Question 10.
If a = 3 and b = 2, then find the value of the following.
(i) a^b + b^a
(ii) a^a – b^b
(iii) (a + b)^b
(iv) (a – b)^a
Solution:
(i) a^b + b^a
a = 3 and b = 2
we get 3² + 2³ = (3 × 3) + (2 × 2 × 2) = 9 + 8 = 17

(ii) (a^a – b^b)
Substituting a = 3 and b = 2
we get 3² – 2² = (3 × 3 × 3) – (2 × 2) = 27 – 4 = 23

(iii) (a + b)^b
Substituting a = 3 and b = 2
we get (3 + 2)² = 5² = 5 × 5 = 25

(iv) (a – b)^a
Substituting a = 3 and b = 2
we get (3 – 2)³ = 1³ = 1 × 1 × 1 = 1

Question 11.
Simplify and express each of the following in exponential form:
(i) 4⁵ × 4² × 4⁴
(ii) (3² × 3³)⁷
(iii) (5² × 5⁸) ÷ 5^s
(iv) 2⁰ × 3⁰ × 4⁰
(v) \(\frac{5^{5} \times a^{8} \times b^{3}}{4^{3} \times a^{5} \times b^{2}}\)
Solution:

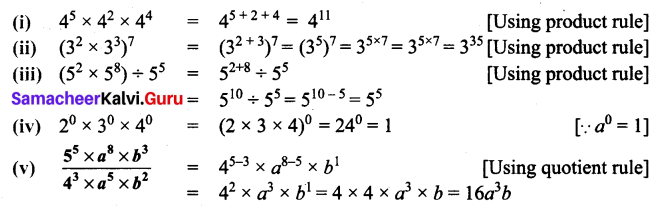
Objective Type Questions

Question 12.
a × a × a × a × a equal to
(i) a⁵
(ii) 5 a
(iii) 5a
(iv) a + 5
Answer:
(i) a⁵

Question 13.
The exponential form of 72 is
(i) 72
(ii) 27
(iii) 2² × 3³
(iv) 2³ × 3²
Answer:
(iv) 2³ × 3²

Question 14.
The value of x in the equation a¹³ = x³ × a¹⁰ is
(i) a
(ii) 13
(iii) 3
(iv) 10
Answer:
(i) a

Question 15.
How many zeros are there in 100¹⁰ ?
(i) 2
(ii) 3
(iii) 100
(iv) 20
Answer:
(iv) 20

Question 16.
2⁴⁰ + 2⁴⁰ is equal to
(i) 4⁴⁰
(ii) 2⁸⁰
(iii) 2⁴¹
(iv) 4⁸⁰
Answer:
(iii) 2⁴¹