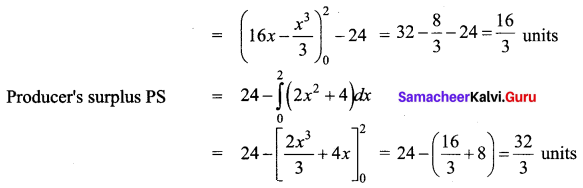Students can download 12th Business Maths Chapter 3 Integral Calculus II Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Additional Problems
I. One Mark Questions
Choose the correct answer.
Question 1.
The area bounded by the curve y = ex, the x-axis and the lines x = 0 and x = 3 is _______
(a) e3 – 1
(b) e3 + 1
(c) e3
(d) e3 – 2
Answer:
(a) e3 – 1
Hint:
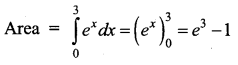
Question 2.
The area bounded by the demand curve xy = 1, the x-axis, x = 1, x = 5 is ______
(a) log 5
(b) log \(\frac{1}{5}\)
(c) log 4
(d) \(\frac{1}{5}\) log 2
Answer:
(a) log 5
Hint:
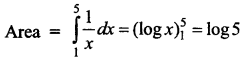
Question 3.
If the marginal cost function MC = 7 – 4x then the cost function is _______
(a) 7x – 2x2 + k
(b) 7 – 4x2
(c) \(\frac{7}{x}\) – 4
(d) 7x – 4x2
Answer:
(a) 7x – 2x2 + k
Hint:
C = ∫MC dx
= ∫(7 – 4x) dx
= 7x – 2x2 + k
Question 4.
The marginal revenue R'(x) = \(\frac{1}{(x+1)}\) Then the revenue function is _____
(a) \(\frac{-1}{x+1}\)
(b) \(\frac{1}{(x+1)^{2}}\)
(c) \(\log \frac{1}{(x+1)}\)
(d) log|x + 1| + k
Answer:
(d) log|x + 1| + k
Hint:
Revenue function R = \(\int \frac{1}{x+1} d x\) = log|x + 1| + k
Question 5.
Match the following.

Answer:
(a) – (iii)
(b) – (iv)
(c) – (i)
(d) – (ii)
Question 6.
If demand function p = 35 – 2x – x2 and demand x0 = 3, then market price p0 is ________
Answer:
p0 = 35 – 2(3) – 32
= 35 – 6 – 9
= 20
Question 7.
If supply law is p = 4 – x + x2 and p0 = 6, then demand x0 is ________
Answer:
x2 – x + 4 = 6
⇒ x2 – x – 2 = 0
⇒ (x – 2) (x + 1) = 0
⇒ x = 2
Question 8.
Say True or False.
(a) Average cost function AC = \(\frac{\mathrm{MC}}{x}\)
(b) Total cost function C = ∫(MC) dx + k
(c) Demand function = P = Rx
(d) Elasticity of demand \(\eta_{d}=\frac{-p}{x} \frac{d x}{d p}\)
(e) Under market equilibrium x0 = p0
Answer:
(a) False
(b) True
(c) False
(d) True
(e) False
II. 2 Mark Questions
Question 1.
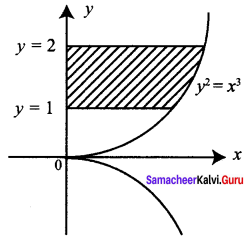
Find the area bounded by the curve y2 = x3 and the lines x = 0, y = 1 and y = 2
Solution:

Question 2.
Find the area bounded by one arch of the curve y = sin ax and the x-axis.
Solution:
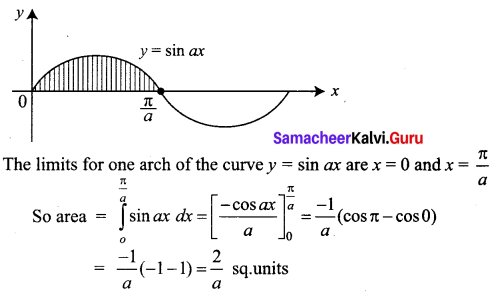
Question 3.
The marginal cost of a commodity is 3x2 – 2x + 8. If there is no fixed cost find the total cost.
Solution:
C = ∫(MC) dx + k
= ∫(3x2 – 2x + 8) dx + k
= x3 – x2 + 8x + k
No fixed cost ⇒ k = 0
So total cost, C = x3 – x2 + 8x
Question 4.
For the marginal revenue function MR = 3 – 2x – x2, find the revenue function and demand function.
Solution:

Question 5.
The marginal cost at a production level of x units is C'(x) = 85 + \(\frac{375}{x^{2}}\). Find the cost of producing 10 extra units, after 15 units have been produced.
Solution:
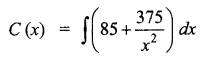
But 15 units have been produced. We have to find the extra cost for 10 units that is, from 15 to 25 units. Hence
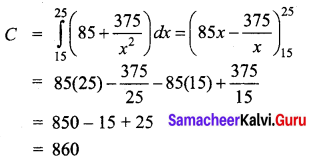
Required cost is ₹860
III. 3 and 5 Marks Questions
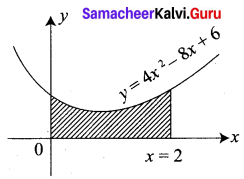
Question 1.
Find the area under the curve y = 4x2 – 8x + 6 bounded by the y-axis, x-axis and the ordinate at x = 2.
Solution:
The shaded area is given by \(\int_{0}^{2} y d x\)
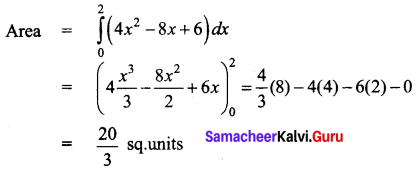
Question 2.
The marginal revenue for a commodity is MR = \(\frac{e^{x}}{100}+x+x^{2}\). Find the revenue function.
Solution:

Question 3.
The elasticity of demand with respect to price p is \(\frac{x-5}{x}\) x > 5. Find the demand function if the price is 2 when demand is 7. Also find the revenue function.
Solution:

⇒ log (x – 5) = -log p + log k
⇒ log (x – 5) + log p = log k
⇒ p (x – 5) = k
When p = 2, x = 1 ⇒ k = 4
Demand function is P = \(\frac{4}{x-5}\)
Revenue R = px or R = \(\frac{4x}{x-5}\), x > 5
Question 4.
The marginal cost and marginal revenue of a commodity are given by C'(x) = 4 + 0.08x and R'(x) = 12. Find the total profit, given that the total cost at zero output is zero.
Solution:
Given that, MC = 4 + 0.08x
C(x) = ∫(4 + 0.08x) dx + k1
= 4x + 0.08\(\frac{x^{2}}{2}\) + k1
= 4x + 0.04x2 + k1
But given when x = 0, C = 0, So k1 = 0
C(x) = 4x + 0.04x2
Now given that MR = 12
R(x) = ∫12 dx + k2 = 12x + k2
Revenue R = 0 when x = 0 ⇒ k2 = 0
R(x) = 12x
Total profit function P(x) = R(x) – C(x)
= 12x – 4x – 0.04x2
= 8x – 0.04x2
Question 5.
The marginal cost C'(x) and marginal revenue R'(x) are given by C'(x) = 20 + \(\frac{x}{20}\) and R’ (x) = 30. The fixed cost is ₹ 200. Find the maximum profit.
Solution:


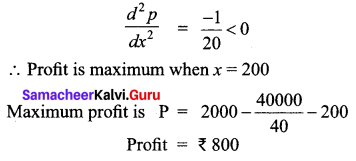
Question 6.
The marginal cost of producing x units is C'(x) = 10.6x. The fixed cost is ₹ 50. The selling price per unit is Rs.5. Find (i) total cost function
(ii) total revenue function and
(iii) profit function.
Solution:
Given C'(x) = 10.6x
C'(x) = ∫(10.6x) dx + k
= 10.6\(\frac{x^{2}}{2}\) + k
= 5.3x2 + k
The fixed cost is ₹ 50
(i.e.) when x = 0, c = 50 ⇒ k = 50
Hence cost function C = 5.3x2 + 50
Now, total revenue = number of units sold × price/unit
Since x be the number of units sold.
The selling price is Rs.5 per unit.
Revenue R(x) = 5x
Profit P = Total revenue – Total cost
= 5x – (5.3x2 + 50)
= 5x – 5.3x2 – 50
Question 7.
The demand and supply functions under pure competition are pd = 16 – x2 and ps = 2x2 + 4. Find the consumer’s surplus and producers’ surplus at the market equilibrium price.
Solution: